Introduction
Split of signal-spikes computer simulated-generated adjoining-neurons is a key problem in extra cellular micro electrode signal-recording from cell-dense-areas of the animal-brain (for instance, hippo-cmapul pyra midal cells). Even though we have different types of software, hardware, firmware windowing-spectral minimization methods, the number of neural cells distinguishable as of single unit single channel signal recordings is small, be in the region of two.1 Normal standard-procedures can not be distinguished amongst analogous- stimulus-amplitudes/spikes initiating as of or on/ or after distinct-neurons intermediate as of the stimulating-sensor and acquiring micro electrode. 2 However, while latest multi channel spikes/data is to be grouped for clustering purposes, such technique needs the effect of preceding, ie.,eralier clustering-of-spike-data gathered under identical-conditions (the identical-electrode, multi neuronal locations, etc.). Such type of necessity enforces and necessitates the constraints or restrictions on the applicability-of the technique to a range-of multi channel spikes-data.
Therefore, we suggest at this juncture a significant enhancement of the stereo trode technique applying through the co-variance, instead of simply the peak-amplitude-ratio, amongst a pattern-tmplate/signature plus a definite spike-acquired by using a multi site micro electrode. 3
Goal
To explore the multi unit multi site micro electrode signal acquisitions of rats hippocampus pyramidal cell layers as well as deep-brain stimulation in anesthetized non-primate-animals using artificial intelligence/machine-learning-techniques (both supervised and unsupervised), signal, as well as clustering-methods..
Methods
Standard traditional windowing-methods distinguish neuronal-spikes by means of referencing their highest-signal-amplitudes primely. Though, limitations of spike-stimulus-amplitudes in the middle of numerous-cells-neurons are complicated to ascertain, e.g., two neural-cells/neurons which are intermediate after the sensor-site might have virtually indistinguishable stimulus-amplitudes/signal-strengths or power of the signal. Mc Naugton,et.al. established the stereo trode technique wherein neuronal-spikes are divided by referring to the probabilistic joint-distribution of highest/peak-amplitudes values achieved by multi channel signal recordings.2 The following Figure 1 depicts is derived which is a combination of signal-decompositin/.
Idea
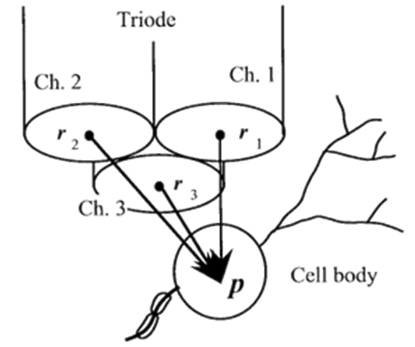
If a succulently strong stimulus is applied to whatsoever part of our or animal body then it gives rise to some excitation and this excitation is due to ion permeability of the membranes. i.e., fluctuations in the membranes. The electrical-action potentials of the aimed neuron is acquired extra cellularly in conjunction with a multi site micro electrode (Figure 2).
Let us consider a spike-generated at the length of time ”T” passing through the aimed neural-cell/ the-neuron positioned at a ‘point’ “p” is derived as
v_n (t) = h (t, p -r_ n) x w (t - T)........ (1)
By way of focussing on the mitigation/ effect of the spatial (temporal) damping factor, the equation (1) is converted in to the
v_ n(t) = h (p - r_ n). w (t – T) + ε_ n (t) ......(2)
By means of minimizing the energy of the error-function, is projected as and then the equation
v_ n (t) ≅ h (p - r_ n). w (t - T) ......(3)
is normalized so that its negative roughly equalizes the -Vepeak of signal-amplitude of evry neural-spikes.
H ̂(p)=(h ̂(p-r_1), (h ̂(p-r_2), (h ̂(p-r_3), … , (h ̂(p-r_N) (4)
4, template-signal/wave forms ought be carefully-chosen, contemplating the range of examined spike of the signal-waveforms 5.
Based-on the unique-template, elastic-template
is derived as w ^γ = ψ (t / γ)...........(5)
where indicates the duration ratio of to i.e., the resistance of is described by the optimum value of is determined so that each spike detected has a maximum-correlation with optimized
Identifying the spikes
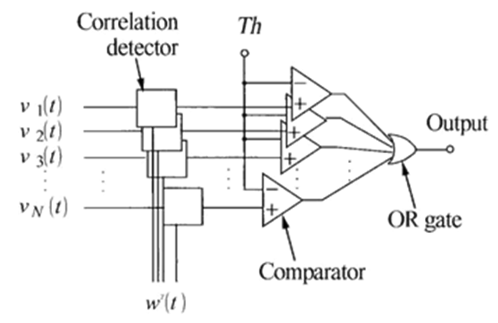
Thecorrelation-technique has been extensively applied for identifying neural/neuronal-spikes.4 In this, the acquired-signals-having high-correlation-coefficients in conjunction through a pattern-matching-template are identified as signal-amplitudes-spikes. 4, 5, 6, 7
The following Figure 3 shows one of the correlation-coefficients-whenexceeds, a amplitude of the signal-spike is believed to have been identified.
Correlation— coefficient computation
To enhance detection of the signal spikes of waveforms, the weight -v e c t o r functor can be used for computation of the c o r r e l a t I o n-c o e f f i c i e n t s. Consequently, by employing the weight functors, the processed—signal at the n - th electrode -point
Where in,
i.e.,
Thus, can change the pattern/signature -signal pattern-template as
We can now thus can generate/compute the correlation coefficient concerning
By changing the expression (11) into the expression (12) through the application of expression (9), as proved in the equation shown below
By connecting the
Damping factorial generation
Through the application of estimating functor
=
Then the equation yield
= -
And then the above expression, i.e., (19) can be computed and while computing it must be set to
Hence, it is set to
Now, if
Spike train potentials
A pair-of-spikes is measured to happen in a gust-under the subsequent constraints: the inter-spike/interval (I S I) is I S I_ b_min, ISI b_max), the corr-coefficient of damping-vectors is (C.C.b_min,1) and attenuation ratio-of-spike amplitudes/signal-strengths ar (attnb_min,attnb_max) which is depicted in the following Figure 4.
Conglomerate-clustering
The cluster is considered as a normal-distribution of N(H;
N(H;
Pi,j
............(22)
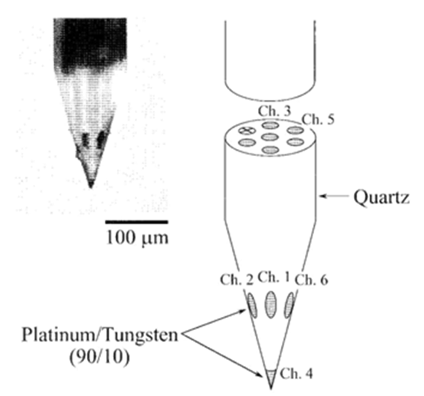
Acquisition of spikes-data
A triode/ or a 7 – core - electrode was employed as a multi-site-electrode which consists of a pack of 3 fine stainless-steel-wires (Figure 2 ; 50
Results and Discussion
This study discussed the equality of a clusters/group with a hippo-campus neuronal or neural-cells. But, the rationality of this conception has not yet resolute. We skilled additional supplementary explorations in which the targeted neuron was distinguished by the collision test. The damping-vectors were resolute by our grouping technique. Subsequently the damping-vectors of the perceived neuronals neuron/neural-cell distilled in a clustering-group that interconnected thriving to one of the cluster/groups in the multi-cluster/group distribution, representing the neuron-cluster communication.
Conclusion
The computational simulation and statistical modeling helps a lot in medical diagnosis especially for effective medical diagnostics in connection with the Brain disease and disorders like Parkinson`s disease, Alzheimer`s, cancer malignancy. So the developed simulation procedure for asynchronously classifying many neural-spikes and neuronal-spikes as of multi site multi-real time channelogrphs of the rats-brain. This simulated technique is more effective and more efficient in investigating multi neural connections in nearby linked neuronal networks.