Introduction
Parkinson disease (or Parkinson`s disease designated as PD) is a complex neuro degenerative disease usually occur in the brains central nervous system – the CNS.1 Even though, the core and key cause of this malady phenomenon is not yet known. Studies shows that the contact of diverse and distinctive processing-circuits of the basal-ganglia and motor-cortex might have concerned and implicated.1, 2 The features, i.e., signs and symptoms of PD appear by the malfunction and death of dopamine-generating cells in an important brain area – the substantia-nigra. The lack of these vital neurons causes various motor disorders including tremor, rigidity, bradykinesia, and postural instability.3
Although, there is currently no certain cure for PD, there are different kinds of treatment options such as medication and surgery to alleviate the disorder manifestations. In recent years, Deep Brain Stimulation (DBS) has been considered as drug therapy.1, 2, 3, 4 Using high frequency (160Hz-200Hz) square pulses (electrical). The stimulus procedure is done during implanted microelectrodes and the current is supplied by a battery-powered implanted pulse generators (IPGs), i.e., the battery like pacemaker is implanted at chest or at abdomen and the IPG at the neck.4 In spite of DBS remarkable performance in providing relief to Parkinson`s, the stimulations may cause some side effects, for instance, cognitive impairment/dementia and postural instabilities, disruption.5 This is mainly because of the existing open-loop DBS systems and lack of understanding about the mechanism of its action. In other words, altered physiological dynamics from adjusting the stimulation parameters, e.g., voltage, stimulus intensity, pulse-width duration measurement and frequency, remains uncertain/and vague.5
Therefore, designing an adaptive closed loop to be able to automatically adjust the stimulation parameters is currently an important research area. Contrary to the direct open loop system that provides a time invariant stimulus current pulse, adaptive/closed loop device would generate a customized stimuli based on the patients’ current behavior, reducing the undesirable dysarthrias which are side effects of the DB stimulation therapy.1, 2, 3, 4, 5
To design an efficient closed-loop device, recognition of dissimilar and unusual PD behavioral tasks rooted in feed-back-signals of PD brain is a main issue/problem to address. DBS provides a chance and an opportunity to gain the access to different brain-waves includes bio signals or biomarkers like beta β-oscillations/local field potentials L.F.Ps, plus acquire unswervingly from the ganglia, i.e., the basal-ganglia.6 Dissimilar activities of PD brain are coded in these waveforms, such that these activities might be differentiated by processing the collected-unruffled signal/waveform. Rooted in different kinds of brain waveforms, hitherto, there have been a number of studies concerning to the detection and classification of singular behavioral tasks of PD brain. Many algorithms have been developed based on the processing of EEG and electro cortico graphy E.Co.G, for instance, epileptic-seizure detections,7 brain switch rooted in motor fantasy or pretend,8 and P-300/speller-paradigm,9, 10 artificial-neural-nets11, 12 and S V M based classifiers mutually by means of feature extractions, pattern matching templates, through wavelets have been successful in perceiving the Parkinson behavior.1, 2, 3, 4, 5, 13, 14 Latterly, S.T.N-β-oscillations (L.F.Ps) have been considered as a useful neural feed-back-biomarker, i.e., bio- signal to identify behavioral activities of the PD brain. The time-series analysis of motor-cortex acquired by E.Cortico.G and S.T.N-L.F.Ps has shown that PD exhibits oscillatory behavior modulated by motor activities, which results in suppression of β-oscillations (~13Hertz-~35Hertz) frequency/spectral-power in motor-tasks. 1, 2 Considering this point into account, a support vector machine -based classifier was proposed by the authors.15 A motor task detection method by applying the L.F. potentials and non linear-regression was shown by authors in.14
An adaptive learning approach based on biomarkers, i.e., the L.F.Ps/signal was suggested by authors in their study,16 in which a model, i.e., hybrid for merging coalescing the support vector machine and probabilistic hidden-Markov-models were applied for the analysis of behavioral clustering of Parkinson`s brain, i.e., the PD brain.
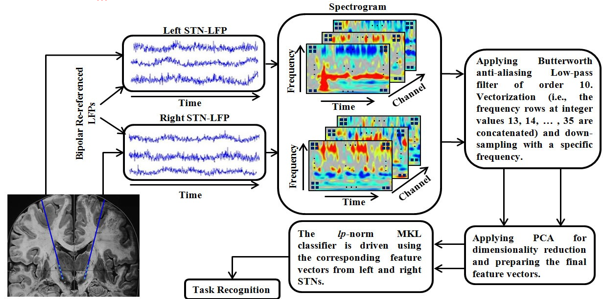
In this study, we demonstrate a l p – n o r m complex Kernel learning C.K.L. or Multi Kernel Learning - the M.K.L.17 approach for the identification of unusual behavioral activities of PD brain by employing the sub thalamic nuclei 30Hz β-oscillations – the L.F.Ps acquired from PD diseased subjects underwent for the therapeutic-surgery of deep brain stimulation. The spectrogram of the raw/unrefined L F P s correlated to every-event was employed to extort the feature-vectors. On the contrary to the formerly demonstrated single kernel S V M - based classifiers, the proposed C.K.L MKL approach utilizes the equivalent and matching biomarkers from PD brains left hemisphere and right hemisphere sub thalamic nuclei’s concurrently. Hence, it will yeild a privileged and superior performance by the proposed-technique/method. Our experimentally investigated findings show that the classification accuracy of the demonstrated method is vigorous even if the feature vectors are largely down-sampled. So, this leads to a lower computational burden. The sections in this study are as follows:
Firstly, signals data acquisition by MER recording-procedure in section 2, secondly, section 3 gives the l p – n o r m C.K.L./M.K.L method and also proposed approach, thirdly, section 4 yields the contrast and quantitative findings, and lastly, section 5 gives the, inferences drawn from this study followed by some observations.
Signal Acquisition
Five 5 Parkinson`s underwent therapeutic deep brain stimulation functional neurosurgery were participated in this bilateral STN-DBS study. The participants had given their informed consent which was approved by the institute ethical committee following the Helsinki principles. The participants performed bilateral MER signal acquisitions using microelectrodes embedded in their brains two sides, i.e., right and left hemispheres subthalamic nucleuses. MER signal acquisitions were done while the PD subjects awakened and all were DBS state off medication.1, 2, 3, 4, 5 The field potentials/biomarkers were acquired from all four contacts of each DBS electrodes. The acquired signals were amplified, and with a 5 kilo Hertz (5kHz) sampling frequency they were digitized, and filtered with band pass filters with 0.5 Hertz lower cutoff frequency and 100 Hertz upper cutoff frequencies, and combined with event markers and subject responses. In the interim, a linked-mastoid common reference was employed for signal acquisitions. And, lastly, the local field potential channels were bi polar re referenced, i.e., between 0 to 1, 1 to 2, and between 2 to 3 prior to the inferences drawn.1, 2, 3, 4, 5, 6, 9 Four kinds of dissimilar tasks were included experimentally investigative: push the button, i.e., press-the-button, movement-of-jaw/the mouth, the vocalizations, and the movement of arm. For every undertaking, a block of numerous repetitions were designed. In terms of the task-initiation, the PD-subjects were cued by an audiosignal. For the press-button, the PD subjects were requested to push the button by adapting their right and/or left thumb. The task of vocalizations comprised of narrating easy and elegant names objects exhibited on the monitor. For the task of the movement of the arm, the Parkinson`s diseased subjects had to raise their arm to contact a tinted target-objective. Lastly the vocalizations were just consisted poignant/touching the jaws devoid of dialogue or idiom or tongue as a contrast to trials of vocalizations.
Materials anMethods
Firstly, a concise examination of the l p – n o r m C.K.L./M.K.L classifier was explained. Followed by the approach of the feature extraction and also the planned and projected classification method is demonstrated.
2.1. L p – n o r m complex Kernel Learning
The CKL has gained to a large extent fame in the pattern matching recognition and templates in artificial intelligence machine learning Faculty owing to its enviable classification ability. Latest studies17, 18 show that C.K.L.-M.K.L shall progress the discriminate control of the support vector machine classifier. The concept behind the C.K.L is to optimally combine the matrix/matrices computed rooted in multi features by means of complex conjugate kernels in support vector machines optimally. 17 Considerably, the Kernel functions plan the features to a new space where they can linearly be separable. The C.K.L-based support vector machines aims to study the resolution decision-boundaries amid singular, i.e., diverse classes and the K e r n e l mishmash permutation weights in a sole and solitary optimization hitch.17, 18 We use the understanding of the C.K.L. classifier referred to as/ termed as a l p – n o r m C.K.L., which proved to be further flexible-supple in choosing distinct K e r n e l mishmashes/permutations. An l p – n o r m C.K.L, wherein-p≥1 is termed as follows.1, 2, 3, 4, 5, 16, 17, 18
where, ϕm(·) maps the feature vector xi to another space based on which the kernel function k(· , ·) = ‹ϕm(·) , ϕm(·)› is defined. The {ωm}`s are the parameters of the decision hyper-planes. M and N are the number of kernels and training samples respectively. C is the penalty parameter and ξi is the slack parameter. Where,
Figure 1
Representation of the proposed human behavioral task classification based on STN-LFPs. Black squares on each spectrogram show how the time-frequency coefficients of the corresponding bipolar signal are down-sampled.
This convex optimization problem17 is solved using its dual form as follows:
Table 1
Assessment of classification accuracy in %. The bold value is the best one in each case. 3. Tasks: push-button, vocalization, and re random segment. 5. Tasks: push button, arm movement
Such that K
where, α=(α1, …, αN)T is Lagrange-vector dual-variables, Y = diag(y1, …, yN) is an NxN diagonal-matrix (yi, label of each sample-xi), K(m) – kernel-matrix corresponding to the mth kernel-function, d=(d1, …, dN)T is the kernel mixture/grouping-vector which prevents the weight of (||ωm||2) in the objective-function of Equation(1), and the other parameters are defined precisely the similar as given for Equation (1).
Feature Extraction
As discussed previously, the time and frequency spatio temporal representation/spectro-gram of the acquired subthalamic nuclei local field potentials STN—DBS as our features are applied here. It was showed that singular behavioral tasks yield different representations in the time-frequency domain.1 Thus, it is an appropriate measure to differentiate various Parkinson`s behaviors. To obtain the spectrogram of a continuous signal, we apply the continuous wavelet transform (CWT) on the bilaterally re-referenced LFPs. We employ the complex Morlet (C-Morlet) mother wavelet which is proven to be a suitable choice for biomedical signal processing: 1, 15
is the C-Morlet mother wavelet. fc and fb are respectively the wavelet center frequency and bandwidth parameter. Since we are interested in analyzing the β frequency components, fc is set here in the range of 13Hz-35Hz.
X (a, b)
where, Xω(a,b) is the CWT of the function x(t) with two variables a (scaling parameter) and b (shift parameter), and
To drive the l p – n o r m MKL classifier, we consider the right and left spectrograms for each event as two feature vectors. First, the two dimensional spectrograms are converted to vectors, and low-pass filtered by an anti-aliasing Butterworth filter of order 10. Then, these feature vectors are down-sampled to keep the computational cost low. Finally, the MKL classifier is applied on these pre-processed data to recognize the behavioral task related to each event. Figure 1 shows the aforementioned procedure graphically.
Results
To evaluate the accuracy of the presented approach, we use the raw LFP data from five unusual/special PD subjects, as demonstrated in the section 2. The computational results of our method are contrasted differentiated via a newly proposed single kernel S-V-M-based method 15 plus we also evaluate the result of 3 distinct kernel-functions on the S-V-M classifier disjointedly and singly: 1. Radial Basis Function (RBF) k(x,y) =exp(γ||x–y||2), 2. Linear function k(x,y)=xTy+c, and 3. Polynomial function k(x,y) = (xTy+c)d.
Note that, x and y are two feature vectors, and γ, c, where, Xω(a,b) is the CWT of the function x(t) with two variables a (scaling parameter) and b (shift parameter). In terms of the lp-norm MKL, we set the parameter p=1.8, and for the SVM-based classifier all the parameters are set so as to achieve the best performance. A10-fold cross validation is implemented in all experiments. Furthermore, in all cases, principal component analysis (PCA) is applied to reduce the dimensionality of data (in each case, 95% of the eigen-values corresponding to the maximum variance direction is kept).
Classification Scheme
The first step to acquire the training and test samples is to specify those parts of the raw LFP data that are related to different events. A time window ranging from 1 sec before to 1 sec after each onset is used to determine the relevant time using Eq. (3).
To evaluate the accuracy of the presented approach, we use the raw LFP data from five different subjects, as described in Section II. The quantitative results of our method are compared with a recently proposed single kernel SVM-based method.15 We also assess the effect of three different kernel functions on the SVM classifier separately: 1. Radial Basis Function (RBF) k(x, y) = exp(γ||x–y||2), 2. Linear function k(x, y) = xTy+c, and 3. Polynomial function k(x, y) = (xTy+c)d. Note that, x and y are two feature vectors, and γ, c, and d are optional constants. In terms of the lp-norm MKL, we set the parameter p=1.8, and for the SVM-based classifier and d are optional constants. In terms of the l p – n o r m MKL, we set the parameter p=1.8, and for the SVM-based classifier all the parameters are set so as to achieve the best performance. A10-fold cross validation is implemented in all experiments. Furthermore, in all cases, principal component analysis (PCA) is applied to reduce the dimensionality of data (in each case, 95% of the eigen-values corresponding to the maximum variance direction is kept).
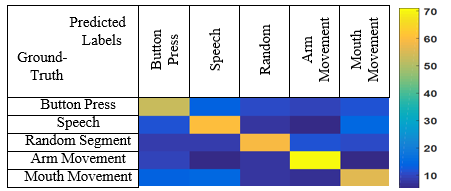
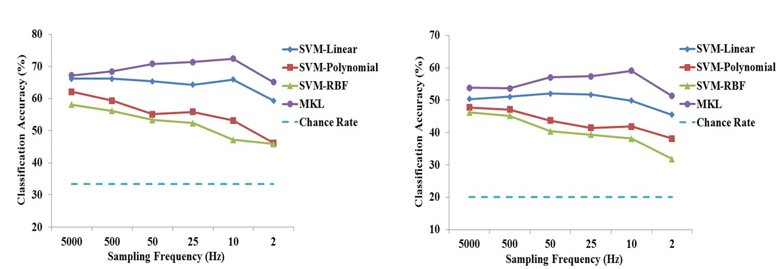
Figure. 2 depicts the classification accuracy of different classifiers vs the sampling frequency (from 5kHz to 2Hz). As seen, the presented l p – n o r m MKL classifier outperforms the other compared classifiers. In the experiments, we observed that the results of the MKL classifier are robust even when the sampling frequency of the feature vectors is drastically low. To measure the robustness of different methods against the size of the feature vectors, all the experiments are redone for different down-sampling rates. Table 1 gives the average classification accuracy of all five subjects for different scenarios (i.e., three and five-task classification and different sampling frequencies). As shown, regardless of the sampling frequency and the number of tasks, the presented MKL-based classifier returns the best results. Figure. 3 provides the average confusion matrix of all subjects with sampling frequency of 10Hz and five-task classification, which summarizes the identification results.
Figure 2
The classification accuracy (%) of different methods. Left and right graphs respectively show the results for 3-task (Speech, Button press, Random segment) and 5-task (Speech, Button press, Arm movement, Mouth movement, Random segment) classification. The reason behind using random segments is to train the classifier to recognize other tasks rather than the existing ones. The “Chance Rate” is to show the qualification of each classifier. If the accuracy is below the “Chance Rate”, it means that the classifier is not a suitable choice; it is nothing but a random operator.
In terms of execution time of the algorithms, using MATLAB 2013a (Mathworks Inc) on a PC with Intel Ci5 CPU (3.4GHz) and 8GB memory, the average training time of each fold of the MKL method for the sampling frequency of 5kHz and 10Hz are about 450s and 6s respectively. The execution time in the test phase for each sample is about 1.5ms and 1ms respectively for the 5kHz and 10Hz sampling rates. For the single kernel SVM classifier, however, the average training time of each fold is about 50s and 0.2s respectively for the aforementioned sampling frequencies, and testing each sample takes about 2ms and 0.3ms. Note that, while 6GB RAM is needed for the 5kHz sampling rate, only 0.25GB memory is used for the 10Hz rate.
Conclusions
In this paper, an l p – n o r m MKL approach for classification of different human behavioral tasks using STN-LFP signal was presented. A feature extraction method based on the time-frequency analysis (spectrogram) of the collected signal was developed. We used the left and right LFPs acquired from the corresponding STNs as two feature vectors. This led to a higher performance with the MKL classifier. The experiments were conducted on five dataset recorded from patients undergoing DBS surgery. The quantitative results confirmed the superiority of the proposed method in almost all cases. In addition, to evaluate the robustness of the classifiers with respect to the size of feature vectors, different down- sampling rates were tested. In contrast to the single kernel SVM-based methods, the proposed MKL approach shows promising results even for very low sampling frequencies. This led to a lower computational burden. Note that, a more accurate classification of the human behavioral tasks would be a precursor for developing future closed-loop DBS systems, which is a cutting-edge research area. Developing a more robust feature extraction method is an interesting extension to this work. Moreover, evaluating the connectivity of different bipolar channels across the DBS leads can be another relevant topic for future research.