Introduction
Microelectrode recording (MER) or microelectrode signals recording of sub thalamic nucleus neurons by means of deep brain stimulation (DBS) local field potentials (LFP) originate as of the cortex or other brain-regions is highly successful for interpreting Parkinson disease (PD) signal analysis acquiescent to elucidation are fetching ever more pertinent. These signals are supposed to emulate S T N neurons action-potential actional-movement also; these potential frequency modulations are coupled to spiking-events. Also verification demonstrates that the potential frequency oscillations are linked by means of neuronal discharge-patterns.1, 2, 3, 4 The amalgamation of better simplicity of contact to LFP signals by means of microelectrode recordings during DBS-surgery1, 3, 4, 5, 6 plus indication of parallel connection of field-potentials by way of neuronal spiking7, 6 generates a want for enhanced plus different techniques of these potentials.
Presently accessible field-potential techniques of signal-analysis methods have mostly depend up on calculations’ in the transform-domain, for instance Phantom plus P S D, cross-correlational (i.e., through FFT) spectral-density, followed by logistic coherence-reasoning.1, 3, 4, 6, 8, 9, 10 By and large, these techniques consistent and dependable for shaping the frequency content of L F P waveforms, and then consequently observing the distinctiveness of the neural-system investigated individual, as well as the information at ease substance of these signals at a range of frequencies, how the neural system is connected with the other areas of the other brain sub-regions, plus these signals are how they linked in the direction of neural signals in the other regions of the brain.1, 3, 4, 6, 8, 9, 10
On the other hand, the techniques have had natural intrinsic limits owing to the non stationary random nature of or temporal-dependencies in the waveforms of L F Ps.,8, 10 and ineffective to differentiate supplementary applicable properties of neural systems, include causality, reliability-stability, also intensity of strengthening afford by the neural-circuit scheduled waveforms of L F Ps. Exact meaning of these distinctiveness is given afterward. Lastly, these statistics are merely evocative, plus build veto development en routed for prognostic-models that may have compensative-merits as scientific research technicalities – engineering and technology plus technological therapeutics advanced.
In this study, the proposed statistical technique applies auto regression (or regressive) modeling (stochastic and random by nature) and benchmark mechanisms from the systems-control theory and identification-sub field. It is a systems-technique of hollow (i.e., curvature) appropriate for random or hit and miss processes curve-fitting. Hence, the goal of this research paper is to study and apply the autoregressive A R modeling and standard techniques from the systems control theory plus system-identification mainly for the application of Parkinson`s disease and dystonic globus pallidal G P neurons injury or damage or movement disorder. The easiest regressions models transmit precedent-events within during a linear-difference-equation towards foresee expectations, i.e., potential-events. The technique approximates and also estimates regression intended for every potential (the L F P biomarker) and then represents the model in the midst of a state space (SS) description.11 The SS depiction necessitates a state progression equation plus corresponding out/put expression, (i.e., equation). The state evolution expression (i.e., equation) gives information in a sequence a propos system permanence (steadiness, stability, etc) and temporal-dependence within the limit Eigen value plus greatest singular value, i.e., highest magnitude of the first, Eigen value, followed by second and third in that order correspondingly.
The technique applied in this work gives insights which might not be achievable unfeasible by means of power spectral density based computational evaluations merely and only which is considered in the midst of the new findings presented which can accessed in this study. The field potentials, i.e., the local-field potentials gathered with the deep brain stimulus electrodes in dystonic subjects with Parkinson`s disease pretentious PD brain areas and then compared with field-potentials recorded as of impervious impassive and unchanged brain-areas. The spectral densities (the power) of these potentials demonstrated not considerable differentiations among the cohorts statistically. On the contrary, equally, our technique proved that the field potentials action plus movement within the unaltered brain-areas had considerably higher and larger temporal dependencies than brain damaged sub-regions and areas. Hence, the results obtained in this study imply that the brain`s pallidal neural areas connected through pretentious Parkinson`s vertebra areas mislay their capability to keep hold of information in sequence plus produce neural-signals which are nearer towards in the direction of pallid shallow (white)-noise, that might reason the experimental pragmatic brain diseases in fastidious scrupulous Parkinson`s and other movement disordered subjects.
Biomarkers
Conventional data-analytics glance at statistical difference by means of cohort, the correlation of the achieved values toward the allusion or indication period, otherwise a transform as of base line rooted in, derived as of percent-variations or else total transforms i.e., variations. Within the pre clinical experimental investigations by means of a extremely small number-of-observations, for instance, n = 9, distinctions amid cohorts require toward large-number to discover an important transform or variation for a biomarker, i.e., biosignal, biomedical, biological or it can also referred to as local field potential occurring due to nearby neurons activations due to the implanted induced deep brain stimulus electrodes.
However, the statistical-variant control of these pre clinical experimental-investigations to detect tiny, nevertheless significant bio marker variations is small. The small statistical-mathematical-variation controls of tiny-experiments gives to supplies to the surveillance that pre clinical investigations often cannot construe, cannot interpret into experimental quantifiable medical-examinations. The data elucidation confront is to discover a procedure to delineate or demarcate a significant consistent signal or waveform whilst the observed-examinations are identically equivalent to 1 plus the possible/probable-signal is tiny.
Because of class dissimilarity`s, pre clinical, pre medical bio marker waveform-signals or local field potentials might be diminutive or petite, and the phase-I bio marker signals might be feeble or pathetic owing to the nature of the chosen normal-control-populace. Accordingly, an enhanced procedure to discover fragile waveform-signals into tiny medical experimental investigations might get benefitted the progress of the drug/the remedial medical treatment. Measure
Materials and Methods – design techniques
We form the field potentials, i.e., L F Ps activity`s acquired through the microelectrode recording through deep brain stimulation leads as the output of a linear time-invariant (LTI) system or LTIS driven and determined by pallid(white) Gaussian white-noise. The model design structural formation pertaining to the statistical signal processing machine learning A R set. Then, we explain the SS demonstration of such prototypes plus précis the computations as of on or after (following) a state-space-model(SSM) that we apply to the field potentials data (i.e., acquired through a sophisticated M E R machine of HFc, of globus pallidal neurons (with induced deep brain stimuli) signal analysis.
Auto regression models of local field potential waveforms
Our machine learning stochastic approach is to compute the non stationary (random nature brain signals) and also study A R stochastic models primarily for inferring local field potential waveforms. In fastidious, we deduce that the potential-signals at discrete-time-bin “k” (indicated by yk, is corresponding output of a linear-system determined and driven-by pallid Gaussian white-noise(ηk) and the bin is at the center. And then linear-model is explained through the below given difference equation (1), together with inputs and corresponding outputs:
Where, “yk” is a random-process indexed by ‘k’, ‘n’ is an order of model-prototype, αi (for i ∈ {1, 2, 3, ..., n}) i.e., model-prototype parameters, and “ηk” is additive-set property(random-generation) ‘0’ mean pallid Gaussian white-noise which we use it as an term of errata(error term). There are numerous techniques which are contemporary for approximating the model-parameters-αi. The least-square (LS) technique is applied for estimating the parameters on training-data of length-“N” to delineate demarcate (following equations 1.1 – 2.3) plus to gauge the goodness of fit on a separate-test-data
plus to reduce || Aα – y || 2. Because, additive-set property-noise term is a Gaussian-term, reducing L S E which is equal to maximizing likely hood function (LHF).12 When the parameters are approximated, then the test-data is applied to corroborate the model-prototype. And then the model-fit is computed by means of evaluating the standardized norm 2 of the model-residual, distincted as
(model-fit) =
The standardized residuals give a quantity of the comparative (proportional and/or relative)qualified amount, i.e., virtual that the calculated - envisaged potential signals (L F Ps) departs as of the definite waveform-signals of local field potentials.
Representing S S
Since these models have inherent and intrinsic properties and hence they them-selves can give information-in-sequence linked to the temporal-dependencies within the data of field potentials, i.e., L F Ps. Especially, the norm 2 para meter-vector yields a concept of the quantity of such-dependencies or ‘m e m o r y’ within the field potentials action and movement, i.e., activities. The superior ||α||2 signify additional dependence on precedent v a l u e s of LFP activity`s, means for a moment k, the yk sturdily dependent lyingon previous values. But, we infer the field potentials activity`s by means of building the corresponding SS representing A R model-prototype firstly.
So, we delineate the state-vector at time “k” as
Therefore, the representing SS is as follows:
Where,
A =
B = 1 0 … (0)T
C =
D = 1
Expression, i.e.,equation(3) defines the S S equation of divergence plus it also explains the corresponding output yk how is it connected with the s t a t e s “x” plus random-noise “η” in the course of the linear-equation, and eventually how the “x” develops.
In control theory and system identification, forming and/or framing a procedure as a linear dynamical system within the SS structure unlocks-up latest opportunity`s for interpreting and inferring the data. Along with that, computational calculations are carried out on the state development milieu, i.e., matrix “A” discloses significant properties of the system-design, together with permanence, steadiness and strength, highest augmentation, plus sensitivity and empathy to upsets. The computational calculations which might be carried out on the “matrix-A” plus what it is that shows every scenario tabularized (Table 1).
Table 1
SS features of the system
It is noted down that the greatest-singular-value i.e., value that is with the highest magnitude signifies the point of memory within the field-potentials activity`s as it is simple to demonstrate that
σmax2 − 1 ≤ ||α||22 ≤ σmax2 (4)
Findings
Local field potentials of pallidal neurons acquired via M E R machine with deep brain stimulations to globus pallidus internas and externas fragments from dystonic cervical, generalized,13 and focal dystonia-subjects with Parkinson`s disease with dystonic-features via no comprehensible mystifying-comorbidities. The goal was discover scientific medical experimental dissimilarities amid neural-waveforms (signals) instigating as of unchanged pallidal brain sub-areas, plus individuals which stems as of pretentious pallidus areas of PD subjects. For comparison purposes we have computed usual power spectral densities to prove that the conventional P S Ds cannot yield the significant differentiation amid 2 cohorts examined statistically p<0.05 through a chi-square conducted χ2@1.3568 by a 2 degree of freedom which is not significant even at 5 %.
Dystnoic subjects signal acquisition through microelectrode recording (M E R system
The electrodes were implanted into the pallidal areas of dystonic subjects and 2 T R plus K W dystonic subjects by means of cervical-dystonia (CD, idiopathic) were received with brain stimulus electrodes deeply in the pallidal parts accordingly with meticulous neurosurgical operation.14, 15 The signals were acquired through micro-electrode recording machine throughout the D B stimulations for a period of 124 per second. Altogether in total, overall there were 12 working unichannel test-trials as of every subject, by an average test-trial length of 124/per second. Single unit activity (S U A) and actional-movement is acquired as well. Embedding the microelectrode in the midst of globus pallidus is confirmed through observing SUA throughout the microelectrode progression. Taxonomy of every channel-signal vista seeing that being pretentious or precious or unnatural or natural unaltered was done through discovering the working-region, for example dexterous hand pincer fingers, forearms-wrists, elbow, etc, connected with every channel-signal acquisition, plus noting-down the occurrence or non occurrence nonexistence of feature-manifestations, signs and symptoms or syndromes of dystonia.
Working areas plus attacked pretention state connected as by means of every acquisition test-trial is given in the table 2. The test-trials are plain resting-interludes; although, the 2 cohorts displayed dynamic-dystonia-syndromes in test-trials, what integrated in voluntary muscle contractions. The sampling frequency of field potential signals were sampled at 25kiloHertz by employing the 16-bit Dynalog (Denmark) analogue to digital converter amplified by means of 10000times plus was filtered with lower-cutoff 10Hertz plus upper-cutoff frequency 10kiloHertz ahead of being accumulated in a file for further processing later. The amplifier-bandwidth: for a typical low pass filter, the upper cut off-frequency is 20kiloHertz and for a typical high-pass filter, the lower cut off-frequency is 0.5 Hertz and it was band pass filtered. The band pass filter with the same frequency ranges applied in this study. The following Table 2 gives the pallidal neural acquisitions areas followed by pretension-state for every test-trial number for the two above designated subjects.
Table 2
Subjects working regions followed by embedding microelectrodes
Model estimation of auto regression
The discretized field-potentials computed in Mat lab (R2018a) version 9.4 with tool box containing various tool-kits, such as, advanced image and (statistical) signal processing, wavelets, neural nets, custom-built-software, etc.
The spectral density was computed and plotted. The computations were mainly for plotting and then for comparing the regression technique through a new customary technique. Every test-trial was divided in to a one second non overlapping parts and then spectral densities were computed by applying the cross correlation Fast Fourier Transform (FFT) and was functional over all segments by means of a windowing technique – hamming window. The purpose of segmenting was selected for mitigating the outcomes of the noised-frequency contents largely inside the field-potentials, i.e., L F Ps, whilst matching necessitates in support of adequate dynamic-range (pixels-resolution) of the frequency.
Computing with autoregression
Twelve subjects potential signals were discretized and for every subject the signals were filtered virtually by employing windowing, i.e., moving average window d e c I m a t i o n algorithmic-module and executed by a digital filter called “finite-impulse-response-FIR” with an order of 2 5 0 and was down sampled to 100Hertz (i.e., the virtual-data). Later, every filtration was divided into twenty-five parts, and every part was divided auxiliary in to instruction and testing data-vectors (i.e., data consisting of both quantum of magnitude and the directional) by the 81 % of the lead of the neighboring signal ensigned or flagged astrain plus sprawling 19 % ensigned like test.
The standardized residual norm 2 value was then calculated computationally to evaluate the model-fit for every A R regression model by exploiting the twenty-five seconds part of the test-data for every subject. The modes that given the results very significantly significant were modes of order-7 plus have-had meant standardized left out was of 0.156 pro P D subject two cohorts – the T R and 0.235 for P D subject K W. Therefore, presumed that these errata is considered for the deducing the inferences in this study.
Mode features of auto regression
For every feature that we attained through our computation (through Mat Lab) is tabularized (Table 1) and every twenty five second seg ment of the field potentials data (the L F Ps data filtered by F I R-digital filters), plus for every mode, order-n = {1, 2, 3, …, n} and the feature-mode by the difference (highly significantly) among pretentious plus impervious brain-areas for two cohorts was greatest-value(singular) which was showed through the distinctiveness in means, un equivocal variance, student-t-test carried out amid precious plus impassive features computationally achieved.
The following Figure 1 shows a demonstration of the largest value (i.e., singular-value) and computationally the outcomes achieved as the for the best-fit model for two cohorts. Also, the figure presents the distinction in the values of the features among unaltered and altered pallidal neural areas for the modes of the seventh-order.
Computing with the power spectral-density
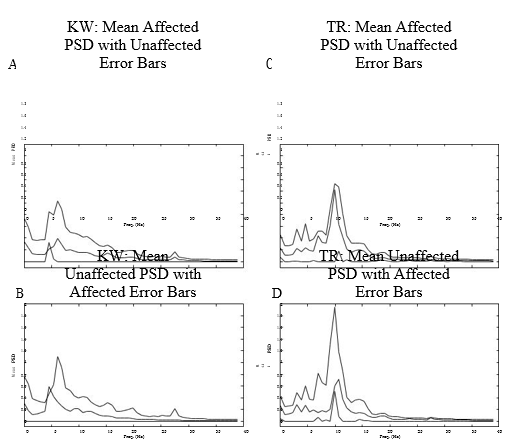
The below Figure 2 depicts the field potential signals data computed for the spectral densities (the power) which is mainly showing the lack of progression for exactly categorizing the potentials (L F Ps) as of pallidal neurons acquisition highlights being altered or unaltered under statistics (2nd-order) only.
The pictures, A,B exhibit mean power-density showed with solid-line at 96% confidence-level-interval athwart for every subject one second potential-signal-segments acquired as of unaltered pallidal neurons-sites, averaged inside the bands-frequencies and C,D exhibit the similar for acquisitions in exaggerated pallidal-neural-sites. Even though perceptible distinctions be present amid the P D subjects, the total-spectra (statistically) considerably and importantly not differing among the unaltered and altered areas of P D brains within two cohorts.
Figure 2
P S Ds – Me a n P S D computational in Mat Lab (depicted with hard-lines), normalized inside band-frequencies, in support of mutually T R(A,B) plus on behalf of K W(C,D). 9 5 % errata (darted-lines) computed as of data of the converse (reverse) exaggeration amplification (hyperbole) condition are exhibited parallelly to demonstrate the short of major distinction among exaggerated plus impassive impervious pallidal-neurons (statistically not-significant).
Discussion
The technique of regression has long been used as an experimental arm of multi variate statisticians. The autoregression is employed in many areas in deed in a myriad of areas and fields (engineering medicine biology etc trans discipline). Researchers10, 11 used a variant of the techniques applied in this study, however select a singular and special way pro the inferences. Further they had employed dynamical multi variate autoregression modes to experiment the coherence stochastic amid the field-potential-waveforms (signals) within the sub thalamic nuclei plus pallidal neurons, by using the electro–encephlo-graphy (E E Gs) waveforms of four classes of α, β, θ, δ, and gamma γ followed by high frequency signals beyond 300 Hertz’s.
We have chosen by considering their study in distinct-course and in different angle by generating the S S system demonstrations of regression modes plus inferring the change-matrix-properties in S growth-expression (i.e.,equation).
The largest-singular-value(LSV) feature of regression-based S S-modes show the highest dissimilarity among altered and unaltered pallidal neural-areas, showing which max(σ(A)) have-had broader-causal semantic-meaning within the perspective inferences of field-potentials. Here in system’s control-theory, the mathematical symbol or equation “max(σ(A))” shows the intensity of temporal-dependencies within the data of two cohorts.
Conclusion
We might have applied P S Ds of L F potential M E R signals that confine power at a range of frequencies in the S T N-neuronal signals waveform, albeit, P S Ds are second order statistics might not incarcerate non-trivial temporal dependencies that exist in the raw-data. The A R models given further insights into Parkinson`s disease conditions behavior which was not possible with P S D alone computationally.
Finally we may conclude that to decode-better, for good health, and for the system’s retort/ feedback distinctiveness, it is indispensable to tame i/p-signal by means of modulating those field potentials movement, action and activity in the pallidal regions. But, down to limits on interventional studies (both S T N, and G P), the induced deep brain stimulation intra surgical-operational experimental-investigative techniques, it is not easy to produce the system i/p stimuli sought to construct, and design further complex prototype-models.
Acknowledgments
The author wish to thank the DST-CSRI funded project, Dept of Science & Technology (DST), Ministry of Science & Technology (MST), Government of India, New Delhi.

